
Most of the time, this is a great convention and it works very well. But these conventions don’t always work in every situation.įor example, one convention suggested by Cohen and Cohen and popularized by Aiken and West is to use three values of the moderator: the mean, the value one standard deviation above, and the value one standard deviation below the mean. There are conventions to help you choose the best values of the moderator for plotting predicted values. Choose the values of continuous moderators intentionally Luckily, plotting the effects of the independent variable at only a few values of the moderator are usually needed to see patterns. Not only would that take a while, the graph would be such a mess, you couldn’t see any patterns. If the moderator itself is continuous, you could potentially choose an infinite number of values at which to plot the effect of the independent variable. Or it too can flip signs, going from a positive slope at low values of the moderator to a negative slope at high values.īut this is difficult to see without a graph. Once again, a positive slope may get larger (or smaller) as the moderator increases. (Yes, that one regression equation really represents many different lines-one for every possible value of the moderator). Moderation says that the slope of the regression line is different at every value of the moderator. So you want to plot the predicted values of those regression lines. If the independent variable is continuous, we measure its effect through a slope of the regression line. It can be hard to discern a pattern in how they differ without seeing it.įor example, the mean difference may get larger as the moderator increases. Moderation says that those mean differences are not the same at every value of the moderator.
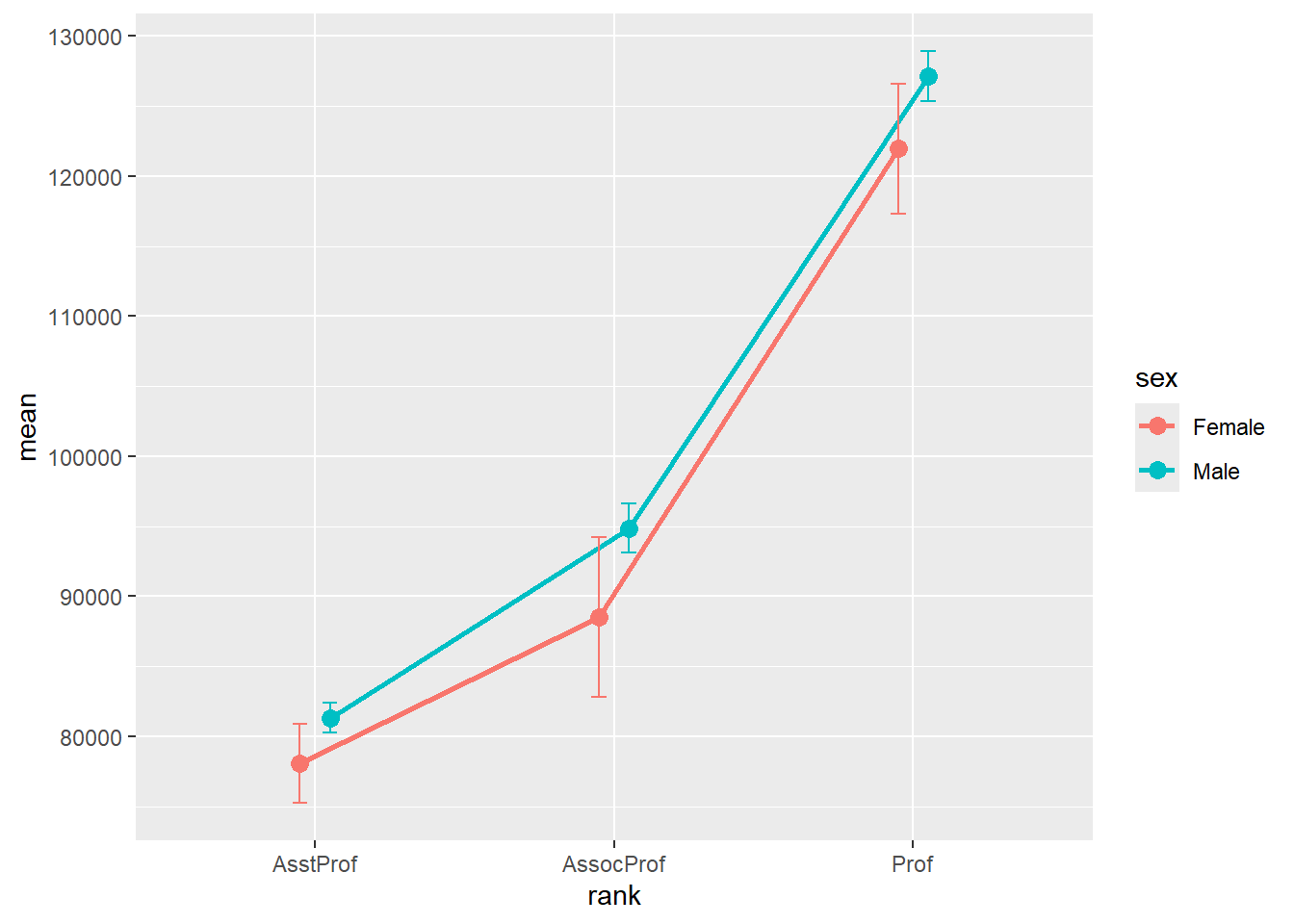
If the independent variable is categorical, we measure its effect through mean differences, and those differences are easiest to see with plots of the means. It helps to see what is the effect of the independent value at different values of the moderator. Moderation effects are difficult to interpret without a graph. But it can help interpretation to think of them that way. You don’t have to interpret one variable as the independent variable and the other as the moderator. Either predictor could be considered to “moderate” the effect of the other. When we speak of interaction, we don’t usually distinguish between independent variable and the moderator. We’re never interested in the effect of the moderator on the dependent variable. In other words, we’re really just interested in the effect of the independent variable on the dependent variable, and this effect is different at different values of the moderator. When we speak of moderation, we usually call the first predictor an independent variable, and the second the moderator. In any case, both an interaction and moderation mean the same thing: the effect of one predictor on a response variable is different at different values of the second predictor. Or because we tend to think of interaction as being part of ANOVA, but not regression.
Perhaps it’s because moderation often appears with discussions of mediation. I have spoken with a number of researchers who are surprised to learn that moderation is just another term for interaction. Realize that moderation just means an interaction
Here are three suggestions to make it just a little easier. Understanding moderation is one of those topics in statistics that is so much harder than it needs to be.


 0 kommentar(er)
0 kommentar(er)
